) obtém-se multiplicando cada dígito pela base elevada à ordem do dígito e somando todos estes valores. çã
Luís Paulo Santos, João Luís Sobral, Alberto José Proença
Dep. Informática, Universidade do Minho, 4719 Braga Codex, PORTUGAL
Tel: +351 53 604479 Fax: +351 53 612954
e-mail: [psantos, jls, aproenca]@di.uminho
Pretende-se com estas sessões apresentar os formatos utilizados pela maior parte dos computadores para representar números (inteiros ou vírgula flutuante).
O capítulo 4 do livro cobre toda a matéria relacionada com este assunto. Estas notas servem apenas para realçar alguns pontos e indicar precisamente quais as secções desse capítulo que são relevantes para acompanhar as sessões práticas: 4.1, 4.2, 4.3, 4.8(parcialmente).
NOTA:Ver secções 4.1 e 4.2 do livro
Os números podem ser representados em qualquer base. Normalmente usamos base 10 (por isso usamos 10 dígitos diferentes), mas poderíamos usar qualquer outra base. Os computadores são máquinas binárias, isto é, só representam 2 valores: 0 e 1. Dizemos por isso que trabalham em base 2 (binário).
Para compreender o que significa a base em que os números são representados é necessário entender o significado da ordem dos dígitos. A ordem de um dígito dentro de um número é dada pela posição que esse dígito ocupa no número, sendo que a ordem do dígito menos significativo é 0. A base utilizada determina o número de dígitos que podem ser utilizados. Base 10 utiliza 10 dígitos, base 2 utiliza 2 dígitos (0,1), base 16 utiliza 16 dígitos (0,1 E,F).
Exemplo
Número: 1532
2 - ordem 0
3 - ordem 1
5 - ordem 2
1 - ordem 3
O valor do número (escrito na base ) obtém-se multiplicando cada dígito pela base elevada à ordem do dígito e somando todos estes valores.
Exemplo
Número: 15326 (base 6)
Número: 
(base 10)
Número: 
(base 13)
Podemos agora converter alguns números escritos em binário para base 10.
Exemplo
Número: 
Para converter de base decimal para base binária divide-se sucessivamente por 2 e tomam-se os restos e o último quociente.
Exemplo
Número: 
235/2 = 117 Resto = 1 /* bit menos significativo */
117/2 = 58 Resto = 1
58/2 = 29 Resto = 0
29/2 = 14 Resto = 1
14/2 = 7 Resto = 0
7/2 = 3 Resto = 1
3/2 = 1 Resto = 1 /* bit mais significativo */
Para adicionar números em binário ver secção 4.3 do livro.
Os processadores utilizam um determinado número de bits para representar um número. A quantidade de bits utilizados determina a gama de valores que podem ser representados. Em binário puro podem-se escrever 
números, sendo 
o número de bits utilizados. O maior inteiro que pode ser representado depende, portanto, do tamanho da palavra em cada processador. Surge assim o problema de somar dois inteiros e obter um número maior do que aquele que a máquina pode representar. Esta situação é normalmente designada por overflow e deve ser tomada em consideração quer pelos programadores, quer pelos desenhadores de microprocessadores (ver pag. 176 do livro).
A base hexadecimal (16) é frequentemente utilizada pelos programadores porque é bastante fácil converter de binário para hexadecimal (e vice-versa) e porque é bastante mais fácil ler um número em hexadecimal do que em binário.
São utilizados 16 dígitos: 0, 1, ..., 9, A, B, C, D, E, F.
Exemplo
Representar 
em hexadecimal.
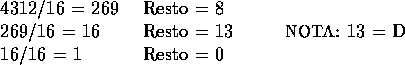
Logo 
D
Exemplo
Representar 
AF
em decimal.
A motivação para usar hexadecimal é a facilidade com que se converte entre esta base e binário. Cada dígito hexadecimal representa um valor entre 0 e 15. Cada conjunto de 4 bits representa também um valor no mesmo intervalo. Então podemos converter aos grupos de 4 bits.
Exemplo
.
Logo 
.
Logo 
NOTA:Ver secção 4.2 do livro
Os computadores lidam com números positivos e números negativos, logo é necessário encontrar uma representação para números com sinal negativo. Uma possibilidade é inverter todos os bits de um número para representar o número correspondente com sinal negativo.
Exemplo
utilizando 8 bits
Invertendo todos os bits obtemos:
O problema desta representação é que existem 2 padrões de bits para o 
. Nomeadamente 
. A solução encontrada consiste em representar os números em complemento para 2. Para determinar o negativo de um número negam-se todos os seus bits e soma-se uma unidade.
Exemplo
utilizando 8 bits
Invertendo todos os bits obtemos:
Somando uma unidade : 
A representação em complemento para 2 tem as seguintes características:
bits é 
. Exemplo
Qual o número representado por 
?
Como o bit da esquerda é 1 este número é negativo.
Vamos inverter:
Somando uma unidade :
Logo 
NOTA:Ver secção 4.2 do livro para detalhes sobre adição, subtracção e overflow.
Como é que podemos converter um número representado em complemento para 2 com bits para um número representado com mais bits? Resposta: basta fazer a extensão do sinal! Se o número é positivo acrescenta-se 0's à esquerda, se o número é negativo acrescenta-se 1's à esquerda.
Exemplo
Representar os seguintes números com 16 bits.
Positivo, logo:
Negativo, logo:
A multiplicação e a divisão têm algoritmos algo complexos que ultrapassam o âmbito destas notas de estudo. No entanto a divisão e multiplicação por potências de 2 realizam-se efectuando shifts à direita ou à esquerda, respectivamente.
Fazer o shift à esquerda uma vez de um número binário corresponde a multiplicar por 2, duas vezes corresponde a multiplicar por 4 e assim sucessivamente. O mesmo se aplica à divisão com o shift à direita.
Exemplo
Dividir 
por 4.
É necessário fazer o shift à direita 2 vezes. 
Multiplicar 
por 8.
É necessário fazer o shift à esquerda 3 vezes. 
Esta regra também se aplica aos números em complemento para 2 desde que se mantenha o sinal.
NOTA:Ver secção 4.8 do livro (pags.225e 243)
Notação científica
A representação de um valor infinito de valores usando uma máquina finita vai obrigar a assumir um conjunto de compromissos, os quais, no caso dos reais, irão afectar não só a gama de valores representáveis, como ainda a sua precisão. A utilização da notação científica, do tipo:
Valor = 
é ainda aquela que permite obter a melhor representação de um núm. real em vírgula flutuante (ou fp na terminologia inglesa) com um núm. limitado de dígitos. O valor do radix é de 10 na representação decimal, e pode ser 2 ou uma potência de 2 na representação interna num computador. A IBM usava nos seus mainframes um radix de 16, pois permitia-lhe aumentar o intervalo de representação de valores; contudo os problemas que tiveram com esta representação (ver 4.11) deram mais força à utilização do valor 2 como radix.
Normalização na representação
A notação científica permite que um mesmo núm. possa ser representado de várias maneiras com os mesmos dígitos (por ex., 43.789E+12 , .43789E+14, 43789E+09). Para facilitar a sua representação - omitindo a necessidade de representar o ponto/vírgula decimal - impõe-se a adopção de uma norma de representação, e diz-se que um dado núm. fp está normalizado quando cumpre essa norma. Alguns autores consideram que um núm. está normalizado quando a mantissa (ou parte fraccionária, F) se encontra no intervalo ]Radix , 1]. Por outras palavras, existe sempre um dígito diferente de 0 à esquerda do ponto decimal.
Exemplo
Normalizando 
Em binário aplica-se exactamente o mesmo princípio.
Exemplo
Normalizando 
Normalizando 
O valor de cada dígito depende da sua posição (ordem) no número. Os dígitos à direita do ponto decimal têm ordem negativa.
Exemplo
Normalizado 
Num exemplo em decimal com 7 algarismos na representação de fp (5 para a mantissa e 2 para o expoente), o intervalo de representação dum fp normalizado, seria em valor absoluto [1.0000E-99, 9.9999E+99]. Existe aqui um certo desperdício na representação de fp usando 7 algarismos, pois fica excluído todo o intervalo [0.0001E-99, 1.0000E-99[. Para se poder optimizar a utilização dos dígitos na representação de fp, aceitando a representação de valores menores que o menor valor normalizado, mas com o menor valor possível do expoente, se designa esta representação de desnormalizada.
Todas as restantes representações designam-se por não normalizadas.
Intervalo e precisão de valores representáveis
Pretende-se sempre com qualquer representação obter o maior intervalo de representação possível e simultaneamente a melhor precisão (relacionada com a distância entre 2 valores consecutivos). Existindo um núm. limite de dígitos para a representação de ambos os valores - F e Exp - há que ter consciência das consequências de se aumentarem ou diminuirem cada um deles.
O intervalo de valores representáveis depende essencialmente do Exp, enquanto a precisão vai depender do número de dígitos que for alocado para a parte fraccionária. Numa representação em binário, a dimensão mínima a usar para fp (que será sempre um múltiplo da dimensão da célula) deverá ser pelo menos 32. Se fosse 16, 1 bit seria para o sinal, e os restantes 15 seriam insuficientes mesmo para representar apenas a parte fraccionaria (daria uma precisão de 1 em cerca de 32 000...).
Usando 32 bits para representação mínima de fp, torna-se necessário encontrar um valor equilibrado para a parte fraccionária e para o expoente. Esse valor é 8 para o expoente - permite representar uma gama da ordem de grandeza dos 1040 - e pelo menos 23 para a parte fraccionária - permite uma precisão de pelo menos 1 em 8 milhões.
Formato binário dum valor em fp
Existem 3 campos a representar nos 32 bits dum valor em fp: o sinal (1 bit), a parte fraccionária (23 bits) e o expoente (8 bits). Para se efectuar qualquer operação aritmética estes 3 campos terão de ser identificados e separados para terem um tratamento distinto na unidade que processa os valores em fp. A ordem da sua representação (da esquerda para a direita) segue uma lógica:
- sinal, S: ficando mais à esquerda, permite usar o mesmo hardware (que trabalha com valores inteiros) para testar o sinal de um valor em fp;
- expoente, E: ficando logo a seguir vai permitir fazer comparações quanto à grandeza relativa entre valores absolutos em fp, sem necessidade de separar os 3 campos: basta comparar os valores como se de valores meramente binários se tratassem;
- parte fraccionária, F: é o campo mais à direita.
O bit escondido
Um valor normalizado tem sempre um dígito diferente de zero à esquerda do ponto decimal. Se o sistema de numeração é decimal, esse dígito pode ser um de entre 9 possíveis; se o sistema de numeração é binário, esse dígito só pode ser um. Assim, e apenas na representação binária, esse dígito à esquerda do ponto decimal toma sempre o mesmo valor, e é um desperdício do espaço de memória estar a representá-lo fisicamente. Ele apenas se torna necessário para efectuar as operações, permanecendo escondido durante a sua representação. Ganha-se um bit para melhorar a precisão, permitindo passar para 24 o núm. de bits da parte fraccionária.
A norma IEEE 754 para valores em fp
A representação de valores em fp usando 32 bits e com o formato definido anteriormente permite ainda várias combinações para representar o mesmo valor. Por outro lado, não ficou ainda definido como representar os valores desnormalizados, bem como a representação de valores externos ao intervalo permitido com a notação normalizada.
A norma IEEE 754 define com clareza estas imprecisões, permitindo uma maior compatibilidade ao nível dos dados no porte de aplicações entre sistemas que adoptem a mesma norma. De momento todos os microprocessadores disponíveis comercialmente com unidades de fp suportam a norma IEEE 754 no que diz respeito aos valores de 32 bits. Aspectos relevantes na norma IEEE 754:
- representação do sinal e parte fraccionária: segue o formato definido anteriormente, sendo a parte fraccionária representada sempre em valor absoluto, e considerando o bit escondido na representação normalizada;
- representação do expoente: para permitir a comparação de valores em fp sem separação dos campos, a codificação do expoente deveria ser tal que os valores menores de expoente (os negativos) tivessem uma representação binária menor que os valores positivos e maiores; as codificações usando complemento para 1 ou 2, ou ainda a representação usando sinal+magnitude, não possuem este comportamento, i.e., os valores negativos têm o bit mais significativo (à esquerda) igual a 1, o que os torna, como números binários, maiores que os números positivos; a notação que satisfaz este requisito é uma notação por excesso, na qual se faz um deslocamento na gama de valores decimais correspondentes ao intervalo de representação de n bits, de 0 a 
, de modo a que o 0 decimal passe a ser representado não por uma representação binária com tudo a zero, mas por um valor no meio da tabela; usando 8 bits por exemplo, esta notação permitiria representar o 0 pelo valor 127 ou 128; a norma IEEE adoptou o primeiro destes 2 valores, pelo que a representação do expoente se faz por notação por excesso 127; o expoente varia assim entre -127 e +128;
- valor decimal de um fp em binário (normalizado): 
, em que S, F e E representam respectivamente os valores em binário dos campos no formato em fp;
- representação de valores desnormalizados: para poder contemplar este tipo de situação a norma IEEE reserva o valor de E = 0000 0000b para representar valores desnormalizados, desde que se verifique também que F <> 0; o valor decimal vem dado por 
- representação do zero: é o caso particular previsto em cima, onde E = 0 e F = 0;
- representação de +/-infinito : a norma IEEE reserva a outra extremidade de representação do expoente; quando E = 1111 1111b e F = 0 , são esses os "valores" que se pretendem representar;
- representação de núm. não real: quando o valor que se pretende representar não é um núm. real (imaginário por exemplo), a norma prevê uma forma de o indicar para posterior tratamento por rotinas de excepção; neste caso E = 1111 1111b e F <> 0 .
Exemplo
Representar 
no formato IEEE754.
O número é negativo logo o bit de sinal é 1.
Não esquecer que 
Normalizando 
Temos 
Para representar a mantissa temos 
Não esquecer que não se representa o 1 à esquerda do ponto decimal.
Sendo o 1
bit o do sinal, os 8 bits seguintes o expoente
e os últimos 23 bits a mantissa.
Exemplo
Sabendo que uma palavra de 4 bytes contém o valor 
,
e que este valor é um número em formato IEEE754 calcule o seu valor em decimal.
O primeiro passo deve ser representar este valor em binário.
Daqui tira-se: sinal = 0
A norma IEEE 754 contempla ainda a representação de valores em fp que necessitem de maior intervalo de representação e/ou melhor precisão, por várias maneiras. A mais adoptada pelos fabricantes utiliza o dobro do núm. de bits, 64, pelo que é também conhecida pela representação em precisão dupla, enquanto a representação por 32 bits se designa por precisão simples. Para precisão dupla, a norma especifica, entre outros aspectos, que o expoente será representado por 11 bits e a parte fraccionária por 52 bits.
This document was generated using the LaTeX2HTML translator Version 0.6.4 (Tues Aug 30 1994) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 numeros0.tex.
The translation was initiated by Joao Luis Sobral on Tue Oct 15 19:03:05 WET 1996